The repository of Python code snippets on Python Fiddle now has 742 posted and counting. Among them, there are several for listing prime numbers. The naive approach by factoring definitely isn’t efficient:

Another approach also contains the hidden double for loop:

Way to go with this one, packing a little program into the regular expression:

If I were to do it, I’d implement it with Eratosthenes’s algorithm.

The work done on Fiddle Salad this month would not have been possible without last month’s planning. Furthermore, Fiddle Salad would not have been my idea if I did not invest time in building Python Fiddle. Python Fiddle was really the end product of 9 years of dreams of running a high performance computer and the result of my experience using Gentoo Linux. So I bought a computer to build Python Fiddle, which also turned out to be necessary to run the latest IDE and development tools to build Fiddle Salad.  When I started working with the Python interpreter in JavaScript,  it was horrendously slow. It took about 20 seconds to load and took up almost 1GB of memory. Any text editor except Vim without syntax highlighting was quick enough to edit the 12MB source code file.

Fiddle Salad is an evolution of both the original idea and code base that belonged to Python Fiddle. Now it is really Fiddle Salad that’s driving the development of Python Fiddle, because they share much of the code base. 

So this is the third major milestone, which I almost gave up on before I embarked on it. Before I started work on this milestone, actually a day or two before I planned, I suddenly noticed huge, discouraging signs. They came as shocking surprises. For example, I discovered a hidden option in an application I have used often before that had some of the functionality I was going to build. If that wasn’t enough, it was actually quite popular and many people probably knew that feature. As another example, I discovered another application that was more innovative in certain aspects than the application I planned to build. I got still more examples, but they aren’t worth repeating here.

As a habit, I reached for my next plan and the best tools I have available. I then realized that I would be throwing away about 8 months of work and the plans for this month, which worked out so well. Although I had no reason and no incentive at all to work on Fiddle Salad, I did so only because I enjoyed every moment of it. I believe that’s what we are all here for, the very drumbeat of the universe.

In the end, those serious signs got swallowed up by my project, as I managed to either include their ideas or integrate them right into it. Fiddle Salad is really the culmination and peak of all live web development environments, having the best features in all of them and in my imagination.

The initial release of PythonFiddle attracted a lot of attention due to an article on SlashDot, one of the best places to post general technology news. Although the first version featured cutting edge technology that would run a Python interpreter in the browser, the general consensus is that it’s good for sharing Python code on the web, but not much else. With some afterthought (or maybe forethought, because this was the original intention), I made a new version for web development.

The new PythonFiddle aims to solve problems with JavaScript by offering Python as a replacement. Developers  prefer class based inheritance to JavaScript’s prototypal inheritance, mostly because it’s mainstream. Writing applications with classes built into the language is helpful in large projects, along with the removal of global scope. For small projects, Python’s pseudo-code like syntax is preferable to the ancient C syntax.

The large collection of third-party tools in JavaScript is not overlooked, as in the case of Google’s Dart programming language. JavaScript libraries such as jQuery can be used directly, others can be added as external resources. With PythonFiddle, web developers who use Python server-side are now able to use the same language client-side. Besides the Python to JavaScript compiler, other advantages PythonFiddle offer include live reloading of the page, Less, and Zen Coding.

The sign the adventure is over is always a return to the starting point after traveling to the other side of the world. In the early days when I wrote the crawler for courses, I gathered faculty links from a table by writing a small scraper for the links. The exact method is not clear, but it could have also been done in numerous other ways. Later, I found only those links when I came back to the project after several months. One reason I may not have recorded the method may be that there were duplicates in them, such as 100’s and 200’s referring to the same page.

At the end of this journey, I have many pages of documentation on the system. However, the system still lacked a way of handling new course pages. Now the system is complete, with only a few lines of code, which would have been impossible without the journey:

This gets a list of faculties from the table by returning a set.

import MySQLdb

db = MySQLdb.connect(user='', db='', passwd='', host='')

cursor = db.cursor()

cursor.execute('SELECT faculty FROM faculties ORDER BY faculty')

db_faculties = [row[0] for row in cursor.fetchall()]

db.close()

set(faculties) - (set(faculties) & set(db_faculties))

By subtracting the intersection of faculties in the database from the faculties in the table, the set of new items are found. The new items may be added to the database. I leave it to the reader.

Not only is this the first step when updating the database, it is a miniature model of the entire application. Thus it wraps everything up in a way that serves a purpose.

The goal of coursetree 2.0 is to leverage the current cloud infrastructure to deliver semantic applications that help users find the information they are looking for.

Features currently planned:

1. Course search that understands what the user wants
2. Filtering of irrelevant links
3. Pattern based degree data mining

Draft implementation strategy:

1. Let Google search index Wikipedia and video links
2. A Bayesian classifier will be used to categorize link content into subjects
3. Template induction and template scraping

Features under consideration:

1. Adaptable prerequisite semantic analysis
2. Fully automated template learning and template extraction
3. Relevant course links/suggested courses

Tenative ideas:

1. Genetic algorithm for grammar rule generation with fitness score assigned according to the total number of parse errors
2. Use hashing algorithms to detect similarity in sections of a page, feed similar sections using wrapper induction to generate template
3. Build map of courses using anti-requisites and display nearest neighbors

Unsuccessful incubation features:

1. Using genetic algorithms to generate templates for wrapper induction
2. Switch to parse trees extract noun phrases for Wikipedia link candidates
3. YQL for video link scraping

Lessons learned and salvaged:

1. Don’t use genetic programming methods where scores cannot be assigned to each individual “program”, as many of the templates were simply fails with zero scores
2. Although in some cases successful (with a comma separated list of noun phrases), in other cases single words were marked as noun phrases in the parse tree instead of a more desirable longer phrase
3. Due to frequent changes in video sites, nested JavaScript callbacks with closures to glue previews to links made the code a target to be recycled

For this part of the project, the goal is to generate a list of courses that meets the requirements for a course from a string stored in the database in a specific format. The entire project was designed so that each component is modular. This way, each component could be written and tested independently, and the complexity of the task is greatly reduced. Likewise, the project consists of so many high level components it appears, at first glance, to be incapable of being one piece. To my surprise, I put together Scrapy + PLY + Django, and it all works beautifully.

Part of the reason these separate components can all come together is that the specifications were set in stone before design, and the design itself (choosing the web framework, scraper, compiler) is tailored with the whole in mind. So for this part, these are the requirements:

From a string of prerequisites separated by commas, with alternatives separated by slashes, generate a list of lists that represents all possible course combinations, without more than one course selected out of each group of alternatives.

Basically, it’s a combination of a list of lists of strings.
 

Once the goal was set, the coding phase was straightforward. Simply understand the meaning of the input, and use a python function to turn it into the specified output.

I’m taking a bite by bite approach to interpreting the course prerequisites from the scraper to make its storage in the database possible. Meanwhile, I already finished the part of it that retrieves the data recursively. The approach I decide to take is the same as building a compiler.

I previously favored a quick approach such as the interpreter pattern.

However, commas in sentences have different meanings depending on the context.

(BIOL 140, BIOL 208 or 330) and (BIOL 308 or 330)

(CS 240 or SE 240), CS 246, ECE 222

The interpreter pattern assumes a symbol only has one meaning. Thanks again to a course I took, I was already familiar with the problem and the solution. Recognizing and defining the problem was the hard part. A quick overview of the steps involved from start to finish:

First step in the compiling process is to tokenize input.  That takes care of blobs such as “Level at least 3A; Not open to General Mathematics students.”. Totally useless in terms of prerequisites. So it should not show up in the token string.

Building the lexer was as simple as specifying the token list, writing regular expressions for them, and setting ignored characters.

Running it gives the output:

LexToken(LPARENS,'(',1,1)
LexToken(DEPT,'CS',1,2)
LexToken(NUM,'240',1,5)
LexToken(OR,'or',1,9)
LexToken(DEPT,'SE',1,12)
LexToken(NUM,'240',1,15)
LexToken(RPARENS,')',1,18)
LexToken(COMMA,',',1,19)
LexToken(DEPT,'CS',1,21)
LexToken(NUM,'246',1,24)
LexToken(COMMA,',',1,27)
LexToken(DEPT,'ECE',1,29)
LexToken(NUM,'222',1,33)

While working on the tree part of the coursetree project, I ran into the question of how to display the course dependencies. I have written a recursive function that returns a recursive list of course prerequisites:

I wanted to turn it into a diagram of course prerequisites and decided 2 flat lists could retain the data:

• a list for the levels
• a list for connections between courses

For example,

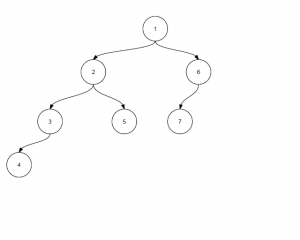
would translate to

and

Separating the Levels

We start off with a recursive list representing the tree structure:

To tackle the problem, I first solved a similar one: flattening a list.
This can easily be done in Scheme, as syntax and type declarations do not get in the way.

Here’s the same code translated into Python:

Unfortunately, flatten in Python produces a hypernested structure for flat lists, as (1 2 3) in Scheme is equibalent to (cons 1 (cons 2 (cons 3 empty))) or (1 . (2 . 3)).

The more serious problem is that it exposes a quirk in Python:

Yes, that means the list disappears after being extended with an empty list . . . one of those unpleasant surprises.
So let’s redefine a flat list in Python:

There is a similarity between this approach and the recursive one: different actions are taken for a list node and other nodes. I used a combined functional and imperative approach to solve the problem:

Connecting the Nodes

We start off with a recursive list representing the tree structure, slightly different from the list for separating the levels:

Again, a mix of recursion and iteration easily solves the problem:

Hopefully, you’ve had fun reading this article and meanwhile came up with a better way to represent the tree as a flat structure.

I’ve had the idea of making a self-updating, navigable tree of Waterloo courses. This is the first step. (Actually, not the first step for me. It started with Django, which had to do with my last work report’s comparison to Zen Cart. Some credit goes to Thomas Dimson for inspiration. He made the Course Qualifier.) The main idea for this step is to gather all the information to be stored in a database. With that (the idea and plan) begins the coding phase:

I wanted to gather the course (“SE 101”), name (“Introduction to Methods of Software Engineering”), desc (“An introduction …”), prereq (“Software Engineering students only”), and offered (“F”) each as separate fields

In order to do that, I wrote a spider to crawl the page:

There are several things to note:

• The prereq field here cannot identify “For Software Engineering students only”. The regular expression only matches the course code.
• Offered, unlike other fields, can contain more than one item
• Prereq may be empty

Finally, the spider pipes its results to an output format. CSV format meets the requirements, as it can be inserted into a database.

Two gotchas:

• Because prereq might be empty, there needs to be an exception handler
• Offered may be variable length. The list needs to be joined to output all of the terms the course is offered.

This part of the project was done in 2 hours with Scrapy. The project can be found in the downloads section.

I asked a question on probably one of the higher traffic forums, and it was answered within an hour. It still took 3 people to put together the answer because one line of code couldn’t work without the other. I had to have about the same level of technical knowledge to make use of the information and ask the question. What made this answer question style different was that the question was answered immediately unlike some other forums I’ve used. You can see it for yourself here:
Python FTP Most Recent File – Stack Overflow

Coincidence? It was on this website that I first heard of dive into python, the online book I used to learn the language. Except I learned dive into python 3 and asked the question from Google. A lot can be said about the use of the democratic process where knowledge matters.